SPECTACLE MAGNIFICATION

KNAPP’S LAW : When a correcting lens is so placed before the eye that its second principle point coincides with the anterior focal point of an axially ametropic eye ,the size of the retinal image will be same as though the eye were emmetropic.
RETINAL IMAGE SIZE(RIS) IN UNCORRECTED AXIAL AMETROPIA:
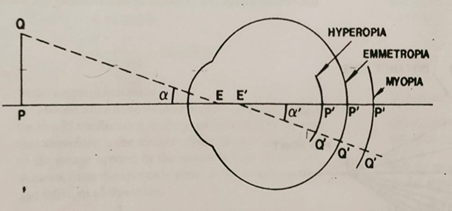
The angle α’ made between the optic axis and the chief ray as it emerges from the exit pupil forms the constant ratio with the angle a between the optic axis and the incident chief ray
Thus RIS is directly proportional to angle ALPHA and also to the axial length
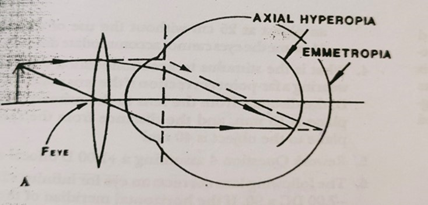
In uncorrected axial ametropia, the size of the retinal image varies only with the axial length of the eye. (H<E<M)

RIS in CORRECTED AXIAL AMETROPIA :
A ray passing through the primary focal point of any lens is refracted so that it emerges parallel to the optic axis
The RIS is determined only by the distance from optic axis to the ray passing through F1
Thus in all cases of purely axial corrected ametropia the RIS is same as Schematic eye

RIS in UNCORRECTED REFRACTIVE AMETROPIA:
Here the power of the eyes optical system varies from one eye to another, but the axial length is equal to that of the Std. Schematic eye
The eyes refractive error has no effect on the angle of incidence of the chief ray so the RIS is same for all
RIS in CORRECTED REFRACTIVE AMETROPIA:
The correcting lens is kept at the F1 of the eye having refractive ametropia which is different than that of the emmetropic eye
The focal length of the hypermetropic eye is greater than emmetropic eye is greater than myopic eye
SPECTACLE MAGNIFICATION :
The spectacle magnification is defined as the ratio of the retinal image size when a person is wearing a spectacle lens (corrected ametropic eye) to the retinal image size when the person is not wearing the spectacles lens (same eye uncorrected).

SM =

SM = Spectacle magnification

BVP = The back vertex power of the correcting lens (D)

h = the distance from the back vertex of the correcting lens to the ocular entrance pupil in meters[vertex distance + 3mm]

t = the center thickness of the correcting lens (m)

n’ = the refractive index of the correcting lens

= The front surface power of the correcting lens

SHAPE FACTOR :
The shape factor is nearly always greater than 1.0, which indicates magnification as because ophthalmic spectacle lenses rarely have anything but convex anterior surface
Spectacle magnification increases with an increase in front surface power or with an increase in lens thickness .
SM decreases with an increase in the index of refraction of the lens material
POWER FACTOR :
Spectacle magnification varies directly with the back vertex power , with the retinal image size increasing with the increasing plus lens power and decreasing with the increasing minus lens power
If plus lens move forward or closer to the eye decreasing the value of h , there is a decrease in retinal image size ,

whereas , when a minus lens is moved closer to the eye there is an increase in image size

SM > 1 for + lens & SM < 1 for -lens

Spectacle magnification is usually expressed as a percent magnification or minification is usually expressed as a percent magnification or minification.
The percent magnification or minification can be calculated form :

Spectacle Magnification (%) = (SM – 1)(100)

RELATIVE SPECTACLE MAGNIFICATION :
Relative spectacle magnification is defined as the ratio of the retinal image size ( for an object at infinity) of the corrected ametropic eye in question to that of the standard emmetropic eye

RSM =

RELATIVE SPECTACLE MAGNIFICATION IN AXIAL AMETROPIA :
For an axially ametropic eye , if the correcting lens is placed so that its secondary principal point coincides with the anterior focal point of the eye , the size of the retinal is the same as if it where the standard emmetropic eye.
In purely axial ametropia , for which ametropia is a result of axial elongation of the globe, the following equation is used to determine the RSM
RSM = Where , RSM = relative spectacle magnification for the axial ametrope ; g = the distance in meters from the anterior focal point of the eye to the correcting lens( g is 0 if the correcting lens is 15.7 mm in front of the eye); and BVP = the back vertex power of the refractive correction (D)
RELATIVE SPECTACLE MAGNIFICATION IN REFRACTIVE AMETROPIA :
In purely refractive ametropia, in which ametropia is a result of an abnormal refractive component or components of the eye, the equation for relative spectacle magnification is the same as that of the power factor for spectacle magnification:
RSM =
Where, RSM = the relative spectacle magnification for a refractive ametrope; d = the stop distance in meters from the correcting lens to entrance pupil = (vertex distance + 3 mm); and BVP = the back vertex power of refractive correction (D).

Note that because d is a distance that is zero or close to zero for intraocular lenses, relative spectacle magnification is then zero or close to it. In other words, the retinal

image of a refractively ametropic eye (eg, an aphakic eye) corrected with an intraocular lens is the same as that of an emmetropic schematic eye
As d becomes larger, the retinal image size becomes slightly smaller for myopes (RSM<1.0) and larger for hyperopes (RSM>1.0)
Therefore, for refractive ametropia , relative spectacle magnification increases with increasing values of d, and is at minimum when d is at minimum.
Therefore, in a situation in which the practitioner wishes to minimize the amount of relative spectacle magnification for an eye that is known to have refractive ametropia, the practitioner should consider prescribing a contact lens.