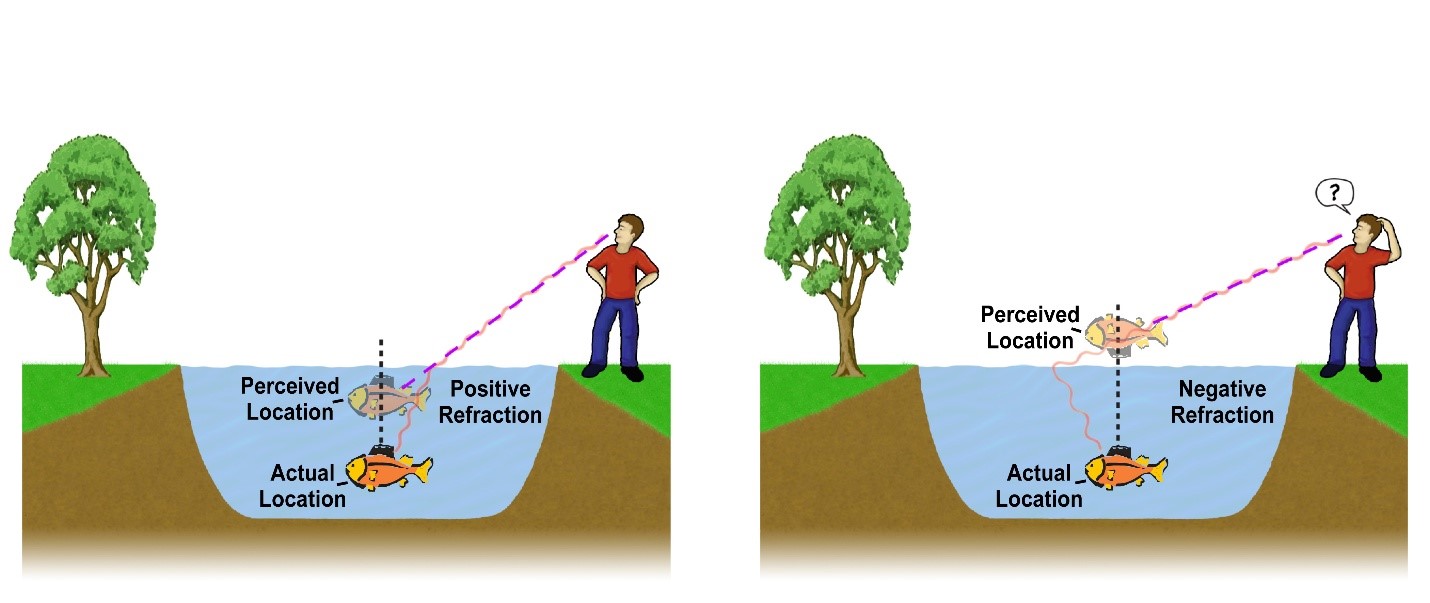
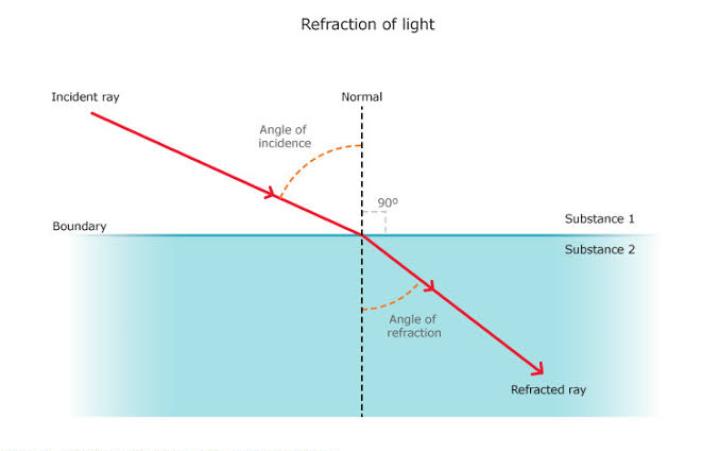
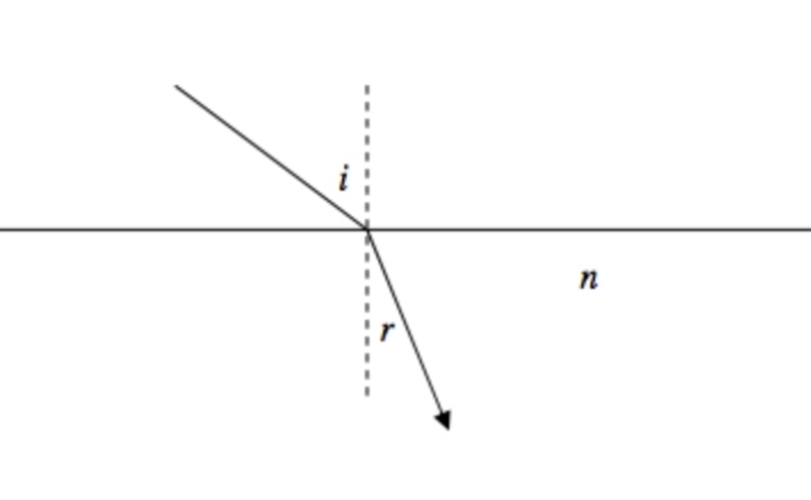
When a ray of light enters a denser medium it is refracted towards the normal in such a manner than the ratio of the sine of the angle of incidence to the sine of the angle of refraction is constant, this constant being called the refractive index n.
This is all right as far as it goes, but we may be able to do better.
- Remember the curmudgeonly professor who will give you only half marks unless you also say that the incident ray, the refracted ray and the normal are coplanar.
The equation—
Sini/sinr = n,
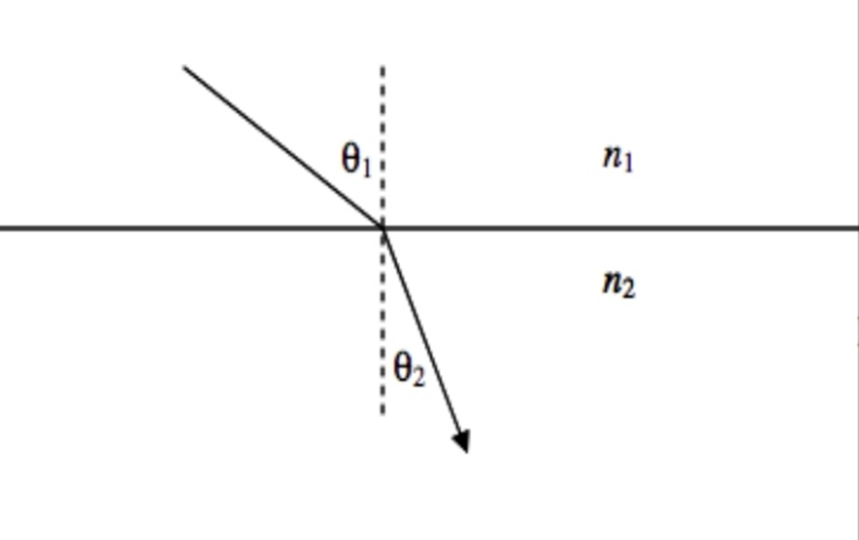
- Where n is the refractive index of the medium, is all right as long as the light enters the medium from a vacuum. The refractive index of air is very little different from unity. If light is moving from one medium to another, the law of refraction takes the form—
Ā Ā Ā Ā Ā Ā Ā Ā Ā Ā Ā Ā Ā Ā Ā Ā Ā Ā Ā Ā Ā Ā Ā Ā Ā n1sinĪø1=n2sinĪø2.
iii. The statement of Snellās law as given above implies, if taken literally, that there is a one-to-one relation between refractive index and density. There must be a formula relating refractive index and density. If I tell you the density, you should be able to tell me the refractive index. And if I tell you the refractive index, you should be able to tell me the density. If you arrange substances in order of increasing density, this will also be their order of increasing refractive index.
In fact light is bent towards the normal in a ādenserā medium as a result of its slower speed in that medium, and indeed the speed \(v\) of light in a medium of refractive index \(n\) is given by v of light in a medium of refractive index n is given by:
N=c/v
Where c is the speed of light in vacuo. Now the speed of light in a medium is a function of the electrical permittivity Ļµ and the magnetic permeability Ī¼ :
V=1/āĻµĪ¼
The permeability of most nonferromagnetic media is very little different from that of a vacuum, so the refractive index of a medium is given approximately by:
NāāĻµ/āĻµ0
Thus there is a much closer correlation between refractive index and relative permittivity (dielectric constant) than between refractive index and density. Note, however, that this is only an approximate relation. In the detailed theory there is a small dependence of the speed of light and hence refractive index on the frequency (hence wavelength) of the light. Thus the refractive index is greater for violet light than for red light (violet light is refracted more violently). The splitting up of white light into its constituent colours by refraction is called dispersion.
Huygensā Construction
Here is a wavefront moving upwards. āLight āraysā are normals to the wavefront.
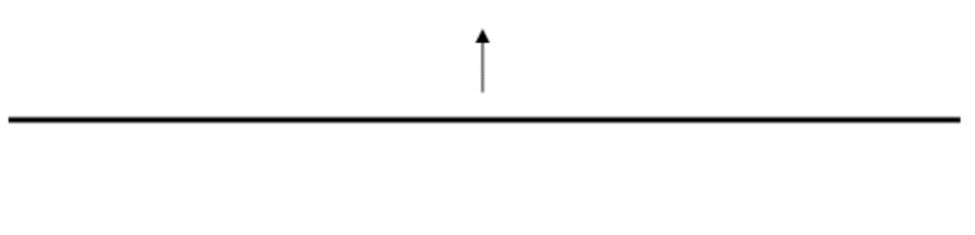
Huygensā construction is a way of prediction what will happen next. It says that you can imagine every point on the wavefront to be a source that generates a little wavelet. Then, after a little time the wavelets look like this ā and the new wavefront is the common tangent to all the wavelets.
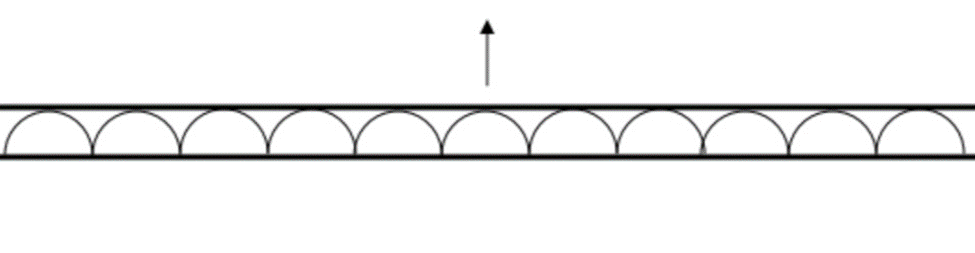
This may sound trivial at first, although much has been written about it ā i.e. whether it represents reality, or is merely a convenient construction. And, if real, what happens to the wavelets in the backwards direction? Weāll not pursue that here, but we can use the Huygens construction as an interesting way to think about Snellās law.
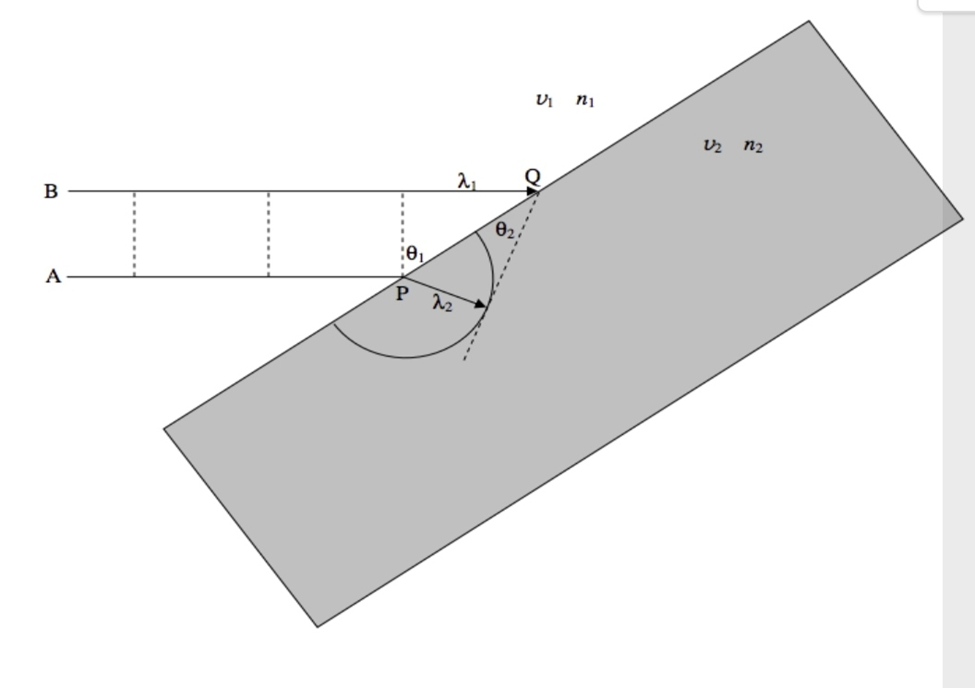
A beam of light of wavelengthĀ Ī»1Ā is approaching a glass block from the left at speedĀ v1 . The dashed lines represent the wavefronts. Ray A reaches the block first, at P. A wavelet is generated at P, moving with speedĀ v2 . The drawing is made for the instant when ray B reaches the point Q. The new wavefront is the tangent from Q to the little wavelet that started at P. The geometry will show thatĀ Ī»1/Ī»2=v1/v2=n2/n1Ā and thereforeĀ sinĪø1=n2sinĪø2 .
