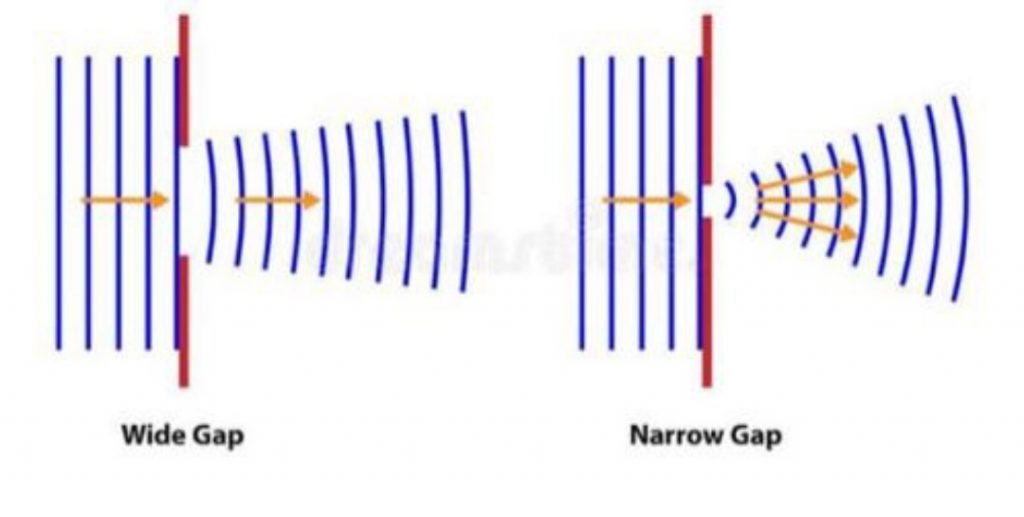
Diffraction is the slight bending of light as it passes around the edge of an object. The amount of bending depends on the relative size of the wavelength of light to the size of the opening. If the opening is much larger than the light’s wavelength, the bending will be almost unnoticeable. However, if the two are closer in size or equal, the amount of bending is considerable, and easily seen with the naked eye.
Diffraction is also the spreading out of waves as they pass through an aperture or around objects. It occurs when the size of the aperture or obstacle is of the same order of magnitude as the wavelength of the incident wave. For very small aperture sizes, the vast majority of the wave is blocked. For large apertures the wave passes by or through the obstacle without any significant diffraction.
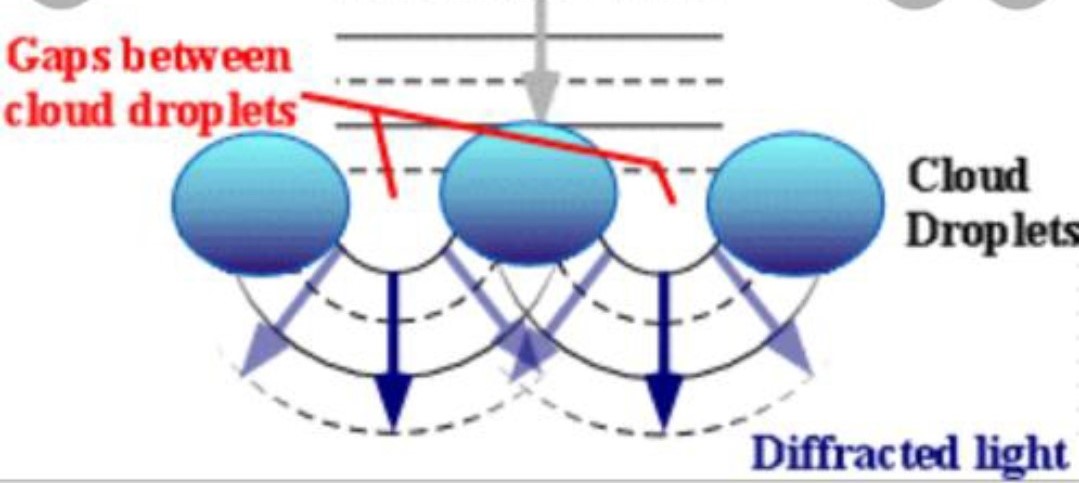
In the atmosphere, diffracted light is actually bent around atmospheric particles — most commonly, the atmospheric particles are tiny water droplets found in clouds. Diffracted light can produce fringes of light, dark or colored bands. An optical effect that results from the diffraction of light is the silver lining sometimes found around the edges of clouds or coronas surrounding the sun or moon. The illustration below shows how light (from either the sun or the moon) is bent around small droplets in the cloud.
Optical effects resulting from diffraction are produced through the interference of light waves. To visualize this, imagine light waves as water waves. If water waves were incident upon a float residing on the water surface, the float would bounce up and down in response to the incident waves, producing waves of its own. As these waves spread outward in all directions from the float, they interact with other water waves. If the crests of two waves combine, an amplified wave is produced (constructive interference). However, if a crest of one wave and a trough of another wave combine, they cancel each other out to produce no vertical displacement (destructive interference).
This concept also applies to light waves. When sunlight (or moonlight) encounters a cloud droplet, light waves are altered and interact with one another in a similar manner as the water waves described above. If there is constructive interference, (the crests of two light waves combining), the light will appear brighter. If there is destructive interference, (the trough of one light wave meeting the crest of another), the light will either appear darker or disappear entirely.
Diffraction can also be referred to a phenomena that occurs when a wave encounters an obstacle. In classical physics, the diffraction phenomenon is described as the apparent bending of waves around small obstacles and the spreading out of waves past small openings. Similar effects occur when light waves travel through a medium with a varying refractive index or a sound wave through one with varying acoustic impedance. Diffraction occurs with all waves, including sound waves, water waves, and electromagnetic waves such as visible light, X-rays, and radio waves. As physical objects have wave-like properties (at the atomic level), diffraction also occurs with matter and can be studied according to the principles of quantum mechanics. Italian scientist Francesco Maria Grimaldi coined the word diffraction and was the first to record accurate observations of the phenomenon in 1665. He coined the term diffraction, from the Latin diffringere, ‘to break into pieces’, referring to light breaking up into different directions. The results of Grimaldi’s observations were published posthumously in 1665. Isaac Newton studied these effects and attributed them to inflexion of light rays. James Gregory (1638–1675) observed the diffraction patterns caused by a bird feather, which was effectively the first diffraction grating to be discovered. Thomas Young performed a celebrated experiment in 1803 demonstrating interference from two closely spaced slits. Explaining his results by interference of the waves emanating from the two different slits, he deduced that light must propagate as waves. Augustin-Jean Fresnel did more definitive studies and calculations of diffraction, made public in 1816 and 1818, and thereby gave great support to the wave theory of light that had been advanced by Christiaan Huygens and reinvigorated by Young, against Newton’s particle theory.
The effects of diffraction are often seen in everyday life. The most striking examples of diffraction are those involving light; for example, the closely spaced tracks on a CD or DVD act as a diffraction grating to form the familiar rainbow pattern seen when looking at a disk. This principle can be extended to engineer a grating with a structure such that it will produce any diffraction pattern desired; the hologram on a credit card is an example. Diffraction in the atmosphere by small particles can cause a bright ring to be visible around a bright light source like the sun or the moon. A shadow of a solid object, using light from a compact source, shows small fringes near its edges. All these effects occur because light propagates as a wave. The speckle pattern which is observed when laser light falls on an optically rough surface is also a diffraction phenomenon. When deli meat appears to be iridescent, that is diffraction off the meat fibers. All these effects are a consequence of the fact that light propagates as a wave.
Richard Feynman said, “No one has ever been able to define the difference between interference and diffraction satisfactorily. It is just a question of usage, and there is no specific, important physical difference between them.” He suggested that when there are only a few sources, say two, we call it interference (as in Young’s slits), but with a large number of sources, the process can be called diffraction.
While diffraction occurs whenever propagating waves encounter such changes, its effects are generally most pronounced for waves where the wavelength is roughly similar to the dimensions of the diffracting objects. If the obstructing object provides multiple, closely spaced openings, a complex pattern of varying intensity can result. This is due to the superposition, or interference, of different parts of a wave that traveled to the observer by different paths.
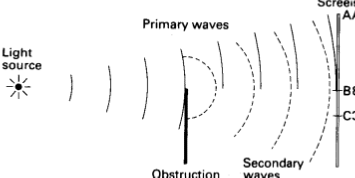
In classical physics, the diffraction phenomenon is described by the Huygens–Fresnel principle that treats each point in a propagating wavefront as a collection of individual spherical wavelets. The characteristic bending pattern is most pronounced when a wave from a coherent source (such as a laser) encounters a slit/aperture that is comparable in size to its wavelength, as shown in the inserted image. This is due to the addition, or interference, of different points on the wavefront (or, equivalently, each wavelet) that travel by paths of different lengths to the registering surface. If there are multiple, closely spaced openings (e.g., a diffraction grating), a complex pattern of varying intensity can result. . The propagation of a wave can be visualized by considering every particle of the transmitted medium on a wavefront as a point source for a secondary spherical wave. The wave displacement at any subsequent point is the sum of these secondary waves. When waves are added together, their sum is determined by the relative phases as well as the amplitudes of the individual waves so that the summed amplitude of the waves can have any value between zero and the sum of the individual amplitudes. Hence, diffraction patterns usually have a series of maxima and minima.
These effects also occur when a light wave travels through a medium with a varying refractive index, or when a sound wave travels through a medium with varying acoustic impedance – all waves diffract, including gravitational waves[citation needed], water waves, and other electromagnetic waves such as X-rays and radio waves. Furthermore, quantum mechanics also demonstrates that matter possesses wave-like properties, and hence, undergoes diffraction
In the modern quantum mechanical understanding of light propagation through a slit (or slits) every photon has what is known as a wavefunction. The wavefunction is determined by the physical surroundings such as slit geometry, screen distance and initial conditions when the photon is created. In important experiments (A low-intensity double-slit experiment was first performed by G. I. Taylor in 1909, see double-slit experiment) the existence of the photon’s wavefunction was demonstrated. In the quantum approach the diffraction pattern is created by the probability distribution, the observation of light and dark bands is the presence or absence of photons in these areas, where these particles were more or less likely to be detected. The quantum approach has some striking similarities to the Huygens-Fresnel principle; based on that principle, as light travels through slits and boundaries, secondary, point light sources are created near or along these obstacles, and the resulting diffraction pattern is going to be the intensity profile based on the collective interference of all these lights sources that have different optical paths. That is similar to considering the limited regions around the slits and boundaries where photons are more likely to originate from, in the quantum formalism, and calculating the probability distribution. This distribution is directly proportional to the intensity, in the classical formalism.
There are various analytical models which allow the diffracted field to be calculated, including the Kirchhoff-Fresnel diffraction equation which is derived from the wave equation, the Fraunhofer diffraction approximation of the Kirchhoff equation which applies to the far field and the Fresnel diffraction approximation which applies to the near field. Most configurations cannot be solved analytically, but can yield numerical solutions through finite element and boundary element methods.
It is possible to obtain a qualitative understanding of many diffraction phenomena by considering how the relative phases of the individual secondary wave sources vary, and in particular, the conditions in which the phase difference equals half a cycle in which case waves will cancel one another out.
The simplest descriptions of diffraction are those in which the situation can be reduced to a two-dimensional problem. For water waves, this is already the case; water waves propagate only on the surface of the water. For light, we can often neglect one direction if the diffracting object extends in that direction over a distance far greater than the wavelength. In the case of light shining through small circular holes we will have to take into account the full three-dimensional nature of the problem.
Diffraction can occur with any kind of wave. Ocean waves diffract around jetties and other obstacles. Sound waves can diffract around objects, which is why one can still hear someone calling even when hiding behind a tree. Diffraction can also be a concern in some technical applications; it sets a fundamental limit to the resolution of a camera, telescope, or microscope.





👏👏
Very informative and interesting Ma’am